Imparare a disegnare da codice

Molto spesso la grafica dei giochi puo' essere composta da forme geometriche molto semplici, si pensi al Pong, il Breakout e il Tetris. Sono tutti giochi in cui gli elementi grafici sono semplici forme geometriche quali cerchi, rettangoli e quadrati.

Questi elementi grafici sono realizzati dal programma per mezzo di funzioni specifiche, che molto spesso sono la semplice conversione in linguaggio informatico di quelle formulette di geometria analitica che ci insegnavano a scuola.

Come nella realta', per disegnare dobbiamo disporre di una qualche superficie idonea.
Nel precedente tutorial "Datti una mossa" ho introdotto molto velocemente un tipo di superficie idoneo e adatto alla nostra causa, la SDL_Surface. Nello specifico, una superficie all'interno del programma di un videogame e' un'area di memoria (ram o video) grande quanto serve, atta a contenere le informazioni che si visualizzeranno sullo schermo quali pixel, grandezza e altezza.

Un pixel e' un quadratino sullo schermo composto dai tre colori primari, Rosso, Blue e Verde (RGB), che insieme ad altri compone le immagini sullo schermo.
Piu' nello specifico e' una struttura dati, contenente i valori cromatici di base del colore che vogliamo utilizzare nelle gradazioni volute. Si possono avere pixel da 8 a 32 bit, nell'ultimo caso sono divisi in 8 bit per colore primario. I primi 8 sono riservati alla trasparenza dell'immagine, spesso questi bit vengono ignorati.

La superficie e' un buffer (array monodimensionale) contenente svariate informazioni come gia' detto, le piu' importanti oltre i pixel sono la grandezza, l'altezza e il pitch.


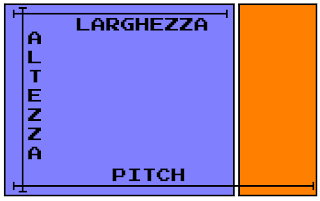
La zona azzurra e' la nostra finestra di gioco, la zona arancione e' l'area rimanente dello schermo.
Il driver video in uso sul sistema crea un buffer che usa per la gestione della grafica sullo schermo, grande quanto la larghezza di risoluzione scelta sul sistema, questo buffer e' detto Pitch (in italiano Campo).
Se la risoluzione di sistema e' 800x600 mentre quella della finestra di gioco e' 320x200, la nostra superficie sara' un buffer di ampiezza [320*200] (Larghezza per altezza) ed avra' una sua posizione nel pitch che sara' grande [800*600].

Questi due buffer pur essendo di base array monodimensionali possono essere intesi come tabelle formate da righe e colonne.
Se per esempio volessimo disegnare un pixel alle coordinate (10,20), ci arriveremo sapendo la lunghezza dello schermo in primis. Moltiplicando la lunghezza dello schermo per il numero di colonne, sapremo in che punto nel pitch inizia la riga che vogliamo (scorriamo l'asse Y con 320*20), ora che siamo alla riga voluta ci basta sommare il valore della coordinata X per il numero di bit per pixel (Bpp, scorriamo l'asse X di un numero di byte corretto) per muoverci alla colonna desiderata (320*20+10).

Si puo' riassumere il lavoro teorico in una pratica funzione:

void drawPixel(int x, int y, int color)
{
 Uint32 bpp, ofs;

bpp = screen->format->BytesPerPixel;
ofs = screen->pitch*y + x*bpp;

SDL_LockSurface(screen);
memcpy(screen->pixels + ofs, &color, bpp);
SDL_UnlockSurface(screen);
 }

La funzione seguente accetta tre parametri, 2 coordinate e un colore.
Le variabili "bpp" e "ofs" sono rispettivamente, BitPerPixel e Offset, facciamo riferimento a strutture interne alla libreria SDL accessibili dalla nostra superficie "screen" per accedere al formato di pixel in uso sul sistema e al famoso pitch.
Prima di disegnare il nostro pixel, e' bene sapere se abbiamo accesso esclusivo alla zona di memoria, dato che puo' essere gestita da terzi o dal driver video. Ricorriamo alla funzione SDL_LockSurface() per bloccare l'accesso alla porzione di memoria ed SDL_UnlockSurface() per ridare l'accesso.
Il valore di colore viene dato in formato esadecimale, la funzione per tanto puo' essere richiamata nella maniera analoga:

drawPixel(10, 10, 0xff0000);

Ora sappiamo come disegnare un pixel sullo schermo, possiamo sfruttare questa funzione con l'ausilio di un'altra per disegnare una linea ad esempio, l'algoritmo qui presentato e' detto l'algoritmo di Bresenham o "Algoritmo del punto di mezzo".
Ci permette date due coordinate di disegnare una linea stilizzata in pixel sulla nostra superficie, questo e' l'algoritmo piu' semplice e utilizzato per questo lavoro. Non si implicano conoscenze matematiche estreme per comprenderne il funzionamento, anche se un po' di nozioni di geometria analitica non guasterebbero.

void drawLine(int x1, int y1, int x2, int y2, int color)
{
int slope;
int dx, dy, incE, incNE, d, x, y;

// Invertiamo la linea se x1 > x2
if(x1 > x2)
{
drawLine(x2, y2, x1, y1, color);
    return; //Usciamo
}

dx = x2 - x1;
dy = y2 - y1;

   // Aggiustiamo l'incremento di linea y-increment per linee in pendenza negativa
if(dy < 0)
{
slope = -1;
dy = -dy;
}
else
{
slope = 1;
}
// Costanti di Bresenham
incE = 2 * dy;
incNE = 2 * dy - 2 * dx;
d = 2 * dy - dx;
y = y1;
// Disegno
for(x = x1; x <= x2; x++)    {
drawPixel(x, y, color);
if(d <= 0)      {
d += incE;
}
else
{
d += incNE;
y += slope;
}
}
}

Per capire questa funzione bisogna avere chiare alcune cose, partiamo dal concetto di base, in geometria analitica, la retta e' rappresentata dall'equazioney=mx+B, dove m e' il coefficente angolare dato dal rapporto della lunghezza di una retta sull'asse X e la sua altezza sull'asse Y in un determinato punto, ovvero deltaX e deltaY.
Questo significa che che possiamo conoscere tutti i punti y di una retta reale in un piano.
Bisogna tenere conto di una cosa, una retta reale puo' avere valori non interi (float) mentre lo schermo di un pc puo' rappresentare punti solo interi nel disegno, cio' gioca a nostro favore anche in termini di velocita'!
La linea reale puo' attraversare la meta' superiore o inferiore di un pixel dividendolo in due, cio' su un pc non sarebbe possibile.
Nell'immagine si nota l'ipotetica linea reale attraversare una griglia di possibili pixel ed il suo equivalente su pc, sono rappresentati anche l'asse deltaX e deltaY per chiarezza.
La parola chiave del nostro discorso e' griglia, questo tipo di immagini per computer sono dette rasterizzate, ovvero basate su griglia.
Come si puo' vedere nell'immagine, per un numero di colonne della griglia, la linea reale attraversa i pixel inferiori, successivamente quelli superiori.
I punti verdi, sono i punti di mezzo, si tiene conto della posizione della linea rispetto ad ognuno di loro, se piu' a destra si disegnera' nel pixel alla loro destra, stessa cosa per la sinistra, sopra o sotto.

Per prima cosa dobbiamo sapere quanto valga "m" nella coordinata maggiore, avremmo il valore della m da deltaX e deltaY, si possono sapere rispettivamente facendo la differenza della coordinata maggiore X con quella inferiore, stesso discorso per la Y.

dx = x2 - x1;
dy = y2 - y1;

Il loro rapporto come gia' detto prima ci da il valore m, quindi la formula diventa ora y=(dy/dx)*x+B. Si puo' spostare il membro dx a sinistra per semplificare, dx*y=dy*x+B*dx ed infine riportare il tutto da un lato solo per avere 0 = dy*x-dx*y+B*dx.
Cio' non basta, siccome ogni punto di mezzo e' tra un pixel e l'altro, si necessita di avere valori interni per ognuno di loro, si moltiplica per 2 entrambi i lati per ovviare alla cosa, F(x,y) = 2*dy*x -2*dx*y +2*B*dx.
Prendiamo d'esempio la funzione matematica appena ricavata e passiamogli come argomenti i valori attuali della X e della Y nel piano piu' un eventuale incremento, l'incremento e' da intendersi come la posizione successiva del nostro pixel attuale nel piano.
Per l'incremento verticale, ovvero Y sara' da considerarsi di 1/2, teniamo conto della Y dato che stiamo lavorando sull'equazione della retta.
F(x+1,y+ 1/2 ) = 2dy(x+1) -2dx(y+1/2) +2*B*dx.

Anche qui possiamo comodamente riscrivere la funzione separando i vari termini e argomenti.
Si moltiplica il 2*dy come elemento unico per ogni elemento delle parentesi tonde e cosi' via anche per la seconda parentesi, semplici nozioni di matematica.
Si avra' una ennesima riscrittura della funzione, F(x+1,y+ 1/2 ) = (2dy*x)+2dy -2dx*y-dx+2*B*dx.

Non basta ancora, possiamo ripulire da un po' di cose questa funzione fino ad avere solamente F(x+1,y+ 1/2 ) = (2dy*x)+2dy -2dx*y-dx+2*B*dx.

Quello che ci rimane sara' la nostra funzione di decisione d=2dy-dx, ci tornera' utile per sapere a quale punto di mezzo la pendenza della linea e' piu' vicino ed eventualmente incrementare o decrementare le coordinate X e Y nella nostra griglia per disegnare il pixel nella posizione voluta.

Per l'incremento e il decremento possiamo rifarci alla funzione matematica di prima, se verso destra (est) si potra' fare la differenza tra il punto successivo e quello attuale incE = F(x+1,y) - F(x,y), mentre per un incremento verticale sempre verso destra semplicemente aggiungendo 1 anche alla coordinata Y (nord-est) incNE = F(x+1,y+1) - F(x,y).
Semplificando le funzioni di partenza otterremo qualcosa del tipo:

incE = 2 * dy;
incNE = 2 * dy - 2 * dx;
d = 2 * dy - dx;

Queste formule nella funzione, se guardiamo avranno utilita' nel ciclo for, questo ciclo scorrera' ogni singola coordinata X della linea e traccera' un pixel alla posizione X corrente e Y corretta.

for(x=x1; x<=x2; x++) {
drawPixel(x, y, color);
  if(d<=0)   d+=incE;  else
  {
d+=incNE;
y+=slope;
  }
}

L'algoritmo pretende che la coordinata finale sia maggiore di quella iniziale, per tanto in caso non lo sia richiama se stessa inviandosi gli argomenti appositamente invertiti.

// Reverse lines where x1 > x2
if(x1 > x2)
{
drawLine(x2, y2, x1, y1);
return;
}

Tiene conto con un apposita variabile invece, della pendenza di linea nel disegno:

// Aggiustiamo l'incremento di linea y-increment per linee in pendenza negativaif(dy < style="font-weight: bold;">{
slope = -1;
  dy = -dy;
 }
else
 {
  slope = 1;
 }

Ora sappiamo come disegnare un pixel e una linea, possiamo anche realizzare cerchi:

void drawCircle(int xc, int yc, int r, int c)
{
 int x = r;
 int y = 0;
 int d = 0;

 for(;;)
 {
drawPixel(xc + x, yc + y, c);
drawPixel(xc + y, yc + x, c);

  if(x != 0)
   {
drawPixel(xc - x, yc + y, c);
drawPixel(xc + y, yc - x, c);
   }

  if(y != 0)
   {
drawPixel(xc + x, yc - y, c);
drawPixel(xc - y, yc + x, c);
   }

  if(x != 0 && y != 0)
   {
drawPixel(xc - x, yc - y, c);
drawPixel(xc - y, yc - x, c);
   }

  if(x <= y)  break;

d += 2*y + 1;
y++;

  if(d > x)
   {
d += 1 - 2*x;
x--;
   }
 }
}

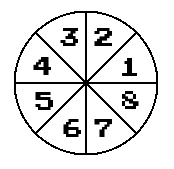Quest'altro algoritmo sempre di Bresenham, presenta molte similitudini con quello della linea, il concetto di lavoro e' pressoche' simile.
Questa funzione di partenza disegna ottavi del cerchio di 45 gradi, cambiando gli argomenti si avranno si avranno anche i rimanenti 7 ottavi rimanenti fino a cerchio completo.

Possiamo lasciar da parte le spiegazioni matematiche, si puo' capire il funzionamento della funzione benissimo analizzando anche una sola parte di essa:

void drawCircle(int xc, int yc, int r, int c)
{
 int x = r;
 int y = 0;
 int d = 0;

 for(;;)
  {
drawPixel(xc + x, yc + y, c);

   if(x <= y)  break;

d += 2*y + 1;
y++;

   if(d > x)
    {
d += 1 - 2*x;
x--;
    }
  }
}

Si potrebbe andare avanti implementando funzioni per le piu' svariate forme partendo da queste tre, ad esempio triangoli, ellissi, rettangoli e via dicendo.
Esistono anche una moltitudine di implementazioni di questi stessi algoritmi piu' o meno efficienti, il mio consiglio e' quello di usare una libreria apposita come standard per questi lavori e anche per risparmiare tempo.
Le librerie piu' usate per questi lavori sono la SDL Gfx o la piu' snella e meno conosciuta SDL Draw, per quest'ultima si deve agire a mano per una installazione come si deve.